(Продолжение. Начало в №3)
Типы данных системы
Простые типы данных
Комплексные числа
Система выполняет операции с комплексными числами. Они записываются в алгебраической форме с мнимой единицей, которая обозначается i (учитывается регистр, то есть используется именно маленькая буква); то есть в виде a+b*i, где а и b - соответственно действительная и мнимая части числа. Например:

Структурированные типы данных
Массивы
Для создания массивов используется функция matrix.
Синтаксис функции:
[Имя матрицы:]matrix([значение элементов в строке, отделяющиеся друг от друга запятой] [,значение элементов в строке, отделяющиеся друг от друга запятой]...)
Значения строк также отделяются запятой.
Следовательно, для создания вектора-строки следует применить функцию так:
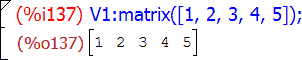
Пример создания матрицы:
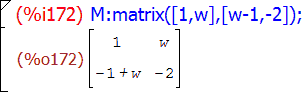
Работу с матрицами обеспечивают также команды пункта главного меню Алгебра и несколько инструментов панели "Statistics".
Например, создание массива с помощью команд пункта главного меню Алгебра осуществляется так:
- Выполнить команду Алгебра > Enter Matrix (Ввести матрицу). Появится окно "Матрица".
- Определить размерность матрицы, а при необходимости и ее тип, например "диагональная".
- В поле "Name" (Имя) ввести имя матрицы.
- Появится окно с матрицей заданной размерности, в котором вводятся элементы матрицы.
- Щелкнуть "ОК".
| Операции с массивами | ||
| Операция | Примечание | |
| М1+М2 | Добавление | Массивы должны быть одинаковой размерности |
| М1-М2 | Вычитание | |
| М1.М2 | Умножение массивов | Массивы должны быть соответствующей размерности: количество столбцов в левой матрице М1 должно равняться количеству строк в правой матрице М2. Результатом будет новая матрица, которая будет иметь такое же количество строк, как и в матрицы М1, и такое же количество столбцов, как и в матрице М2 |
| М1*М2 | Поэлементное умножение массивов или умножение массива на скаляр | Массивы должны быть одинаковой размерности. Векторы должны иметь одинаковую структуру, то есть быть оба или столбцами или строками. При выполнении действия умножения двух массивов результатом будет массив такой же размерности, каждый элемент которого является произведением элементов массивов с одинаковыми порядковыми номерами |
Размерность матрицы очень просто изменить. Для этого следует установить курсор среди ее значений и удалить ненужные строки или столбики. При этом следует помнить, что количество элементов в каждом столбце или строке должно быть одинаковым. Размерность матрицы изменяется также с помощью соответствующих функций:
- Увеличение количества столбцов. Используется функция addcol, имеющая два аргумента: имя массива и новые элементы в виде списка или матрицы. Список элементов записывается в квадратных скобках; при этом каждый элемент отделяется друг от друга запятой. Следует не забывать применить перед этим оператором действие присвоения для массива, для которого происходит увеличение количества элементов. Например, если нужно прибавить к массиву V1 два элемента (9 и 10), то функция будет иметь вид:
V1: addcol(V1,[9,10]); - Увеличение количества строк. Используется функция addrow, имеющая два аргумента: имя массива и новые элементы в виде списка или матрицы. Например, если нужно прибавить к массиву V1 еще одну строку с элементами 1,2,3,4,5, то функция будет иметь вид:
V1: addrow(V1,[1,2,3,4,5]); - Уменьшение количества столбцов. Используется функция submatrix, имеющая синтаксис:
submatrix(Имя матрицы; начальный номер удаляемого столбца; конечный номер удаляемого столбца).
Например, если нужно удалить из матрицы V1 6-й и 7-й столбец, то функция будет иметь вид:
V1: submatrix(V1, 6,7); - Уменьшение количества строк. Используется функция submatrix, имеющая синтаксис:
submatrix(начальный номер удаляемой строки, конечный номер удаляемой строки; Имя матрицы;)
Для обращения к конкретному элементу массива М используется выражение M[j, i], где М - имя массива, j - номер строки и i - номер столбца. При этом такая запись распространяется и на вектор (одномерный массив), и на матрицу (двумерный массив). Для одномерных массивов просто добавляется еще один элемент: для вектора-столбца это будет номер строки, а для вектора-строки - номер строки. Понятно, что в обоих случаях этот номер всегда равен "1".
Например, если нужно сложить значение второго элемента вектора-строки V0 и четвертого элемента вектора-столбца V1, то это осуществляется так:
V0[1,2]+V4[4,1];
Все значения элементов массива могут быть одновременно изменены на одно и то же значение. Для этого необходимо после имени массива добавить знак математической операции и число, на которое нужно изменить все элементы массива. Например, нужно создать новую матрицу, все элементы которой будут равняться "1". Это может быть осуществлено путем создания матрицы, например, с именем М7, все элементы которой равняются "0", а потом использованием оператора:
M7: M7+1;
| Специальные функции для создания матриц | |
| zeromatrix(m, n) | Создание матрицы размерностью m*n, все элементы которой равняются "0" |
| ident(n) | Создание единичной квадратной матрицы размерностью n*n (все ее элементы равняются нулю, кроме элементов главной диагонали, значение которых равняется "1") |
| diagmatrix(n, x) | Создание диагональной квадратной матрицы размерностью n*n, элементами главной диагонали которой являются значения переменной x; а все другие ее элементы равняются "0" |
Матрицу также можно создать автоматически по определенному алгоритму. Для этого следует выполнить команду Алгебра > Generate Matrix from Expression (Генерировать матрицу из выражения), после чего появится окно "Создать матрицу". В поле "matrix[i, j]" вводится математическое выражение, согласно которого и формируются элементы матрицы. Если в текущей сессии предусматривается использовать матрицу несколько раз, то в окне "Создать матрицу" целесообразно также задать имя матрицы. Такой вариант создания матрицы эквивалентен использованию циклов в языках программирования.
Построение графиков
Графические возможности системы достаточно скромны, но все же она позволяет строить графики трех форматов:
- Gnuplot graph. Используется при применении встроенных функций построения графиков. Имеет собственную систему команд, может работать интерактивно (в режиме командной строки) и выполнять скрипты.
- Встроенный. По умолчанию предлагается во время выбора инструмента построения графиков на панели "General Math" или по команде Plot > Plot 2d....
- Openmath. Система разметки математической семантики, которая назначена дополнить MathML. MathML (от англ. Mathematical Markup Language - язык математической разметки) - это дополнение XML, которое используется для представления математических символов и формул в документах WWW.
| Функциональные возможности графиков | |||
| Gnuplot graph | Встроенный | Openmath | |
| Копирование в буфер обмена и вставка из него в другие документы | + | + | - |
| Изменение размеров графика | + | - | - |
| Изменение цвета фона | + | - | |
| Форматирование масштабных ординат, легенды | + | - | - |
| Изменение цвета, типа и толщины линий | + | - | * |
| Сохранение в форматах | - | JPG, BMP, PNG | PS |
| * Возможно конфигурированием, после чего заданные параметры применяются для всех новых создаваемых графиков. | |||
Формат построенного графика можно изменить. Для этого следует выделить команду для построения графика, выполнить команду Plot > Plot Format и ввести название другого формата графика в поле "Введите новый формат графиков" в окне "Формат графика".
Двумерная (2D) графика
Двумерные графики строятся с помощью функции plot2d.
Синтаксис функции:
plot2d(y(x), [x, xmin, xmax])
где y(x) - функция от x, значения которой изменяются на интервале от xmin до xmax.
Обязательными являются все четыре аргумента, при этом только первый аргумент (при условии, что график строится только для одной функции) может быть записан не в скобках, все другие аргументы записываются в квадратных скобках. Это связано с тем, что аргументами функции являются не отдельные переменные-параметры, а списки, для записи которых используются именно квадратные скобки. Например:
plot2d(sin(exp(x)),[x, 0,4]);
На одной координатной плоскости можно одновременно вывести графики нескольких функций. В этом случае первый аргумент plot2d содержит перечень этих функций и записывается в квадратных скобках.
Например:
plot2d([x^3-4*x^2+x, sin(x)],[x, - 1,4]);
Еще проще строить функции при помощи инструментов "График 2D" и "График 3D" панели "General Math" или по команде Plot > Plot 2d... (Plot 3d). Использование этих команд инициирует появление окна "График 2D" или "График 3D". В этом окне пользователь имеет возможность определить ряд параметров, в частности:
- Начальное и конечное значение изменений для переменных x и y.
- "Число точек" указывает, сколько опорных точек используется для построения графика.
- Опции. Это дополнительные действия, которые можно применить к графику. Их определение начинается с ключевого слова "set". Например, "set grid" задает в графике вывод линий масштабной сетки, а "set size ratio 1" выравнивает масштабы по осям координат: это будет полезно, когда строится круг и нужно, чтобы график строился действительно как круг, а не как овал. Следует заметить, что построение круга в виде овала связано с тем, что разрешающая способность монитора по горизонтали и вертикали является разной, поскольку пиксель не является "круглым".
После формирования график появляется в специальном окне, а автоматически сгенерированная команда построения графика, которая имеет синтаксис wxplot2d - в рабочем документе.
Каждая функция plot инициирует построение графика (или графиков) в новом окне.
Редактирование графика
Нажатие мышью на пиктограмме окна в его заголовке для графиков формата gnuplot открывает меню, пункт "Option" которого содержит команды для форматирования графика: изменение цвета фона, стиля линий, шрифта и т.п.
Последней командой пункта "Option" является "Update \..\wgnuplot.ini". Все изменения, осуществленные во время форматирования графика, являются временными и касаются только графика, для которого осуществляется форматирование. Выполнение пункта "Update \..\wgnuplot.ini" приводит к тому, что изменения запоминаются в файле параметров, применяемых для графиков автоматически, и для всех последующих графиков эти изменения будут применяться по умолчанию.
Для изменения параметров уже построенного графика любого типа следует установить курсор на имени функции для построения графика и щелкнуть "График 2D" на панели "General Math". Это приведет к появлению окна "Графики 2D", в котором, как отмечалось ранее, можно изменить ряд параметров.
Построение графика в полярных координатах
Для этого сначала следует загрузить пакет расширенных графических возможностей, который осуществляется по команде load(draw). В ответ система должна ответить, что она осуществила доступ к нужному файлу:
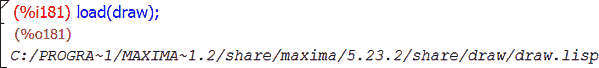
Для построения графика в полярных координатах применяется функция draw2d со следующими аргументами:
- user_preamble = "set grid polar", // построение в полярных координатах
- nticks = n, // n - число точек
- xrange = [dx1, dx2], // диапазон изменения x
- yrange = [dy1, dy2], // диапазон изменения y
- color = red, // цвет
- line_width = k, // ширина линии, которой строится график
- title = "общее название графика",
- polar(функция, переменная, нижняя_граница _переменной, верхняя_граница _переменной) // функция построения графика
Обязательными являются первый и последний аргументы функции. Первый инициирует построение графика в полярных координатах, последний (polar) - это функция, по которой строится график.
В свою очередь, аргумент polar также имеет несколько аргументов:
- Функция для графика. В математике в ее роли принято использовать греческие буквы. Эти буквы изменяются на имена-эквиваленты, например theta.
- Аргумент функции (угловая координата).
- Начальное значение угла.
- Конечное значение угла.
Например:
draw2d(user_preamble = "set grid polar" nticks = 200 xrange = [- 1000,1000], yrange = [- 100,100], color = red line_width = 3 title = "Hyperbolic Spiral" polar(theta*theta, theta, 1,10*%pi) )$
Трехмерная (3D) графика
Для построения изображений трехмерных объектов используется функция plot3d.
Синтаксис функции:
plot3d(z(x, y), [x, xmin, xmax], [y, ymin, ymax], дополнительные опции)
где z(x,y) - функция от x, y, значения которой изменяются от xmin до xmax и от ymin до ymax.
Например:
plot3d(((x - 10)/5)*((y - 10)/5),[x, 0,20],[y, 0,20]);
На одной координатной плоскости можно одновременно построить до трех функций. В этом случае перечень функций записывается в квадратных скобках: plot3d ([функция1, функция2, функция3], [переменная 1, нижний предел переменной, верхний предел переменной], [переменная 2, нижний предел переменной, верхний предел переменной], дополнительные опции).
Редактирование трехмерного графика осуществляется так же, как и двумерного.
Трехмерная поверхность может быть заменена градиентным переходом цветов. Для этого следует применить опцию "set view map".
Валерий ФЕТИСОВ






















Комментарии
Спасибо Вам огромное за такие статьи!
Продолжайте, очень нужна такая информация об этом свободном математическом пакете.
Особенно в Рунете
Спасибо за добрый отзыв. И это еще далеко не последняя статья.