Не появись в "КВ" статья Быченкова А.В. "Забытые криптоалгоритмы" ("КВ" №36 1999), не было бы и этой заметки. Хочу выразить благодарность автору за ясность изложения и газете "КВ" - за то, что она находит на своих полосах место для серьезных статей по криптографии. Я работаю программистом и упомянутая статья, наряду со статьями за подписью Black Prince, доставила мне подлинное удовольствие. Благодаря этим публикациям у меня, как у человека, мало знакомого с криптографией и криптоанализом, сформировалось первоначальное представление об этой области.

Если Вас, дорогой читатель "КВ", волнует тема защиты информации, то, я полагаю, Вам будет любопытно узнать о способах ее кодирования и расшифровки. В статье "Забытые криптоалгоритмы" был изложен алгоритм Меркли-Xeллмана, и я не удержался от соблазна реализовать его в Delphi. Вкратце напомню этот алгоритм.

Сообщение из n бит, представляющее собой бинарный массив C_n, шифруется следующим образом:

1. Создается так называемый "закрытый" ключ, представляющий собой неубывающий массив чисел A_n.
2. 2. Подбираются три числа m, w и u, удовлетворяющие следующим условиям:
   · Число m больше суммы всех элементов Аn.
   · Число w взаимно простое с m.
   · Число u такое, что u*w mod m = 1.
   b_i=(a_i*w) mod m.
3. По следующей формуле вычисляется массив чисел Bn, называемый "открытым" ключом:
   
   
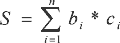
4. Вычисляется скалярное произведение, где c_i - биты сообщения. Число S и представляет собой зашифрованное сообщение С_n.

Расшифровка сообщения производится следующим образом:

1. Вычисляется число P = S*u mod m.
2. Число Р раскладывается по A_n. Решение этой задачи и будет исходным сообщением C_n.

В цитируемой статье был также приведен пример шифрования сообщения длиной в один байт (n=8). Я предпринял попытку реализовать данный криптоалгоритм для n>8. Такое желание вполне объяснимо.

Информацию можно считать защищенной, если ee не удается расшифровать за то время, пока она актуальна. Следовательно, "защитить" - значит попытаться увеличить время расшифровки. Взломщик может воспользоваться криптоанализом, но увеличение длины блока шифруемого сообщения, по крайней мере, увеличит время полного перебора вариантов. Ведь недаром для определения двух простых чисел, использованных в 512-битном ключе RSA Data Security, потребовалось 5.2 месяца и 292 компьютера (Андрей Золотарь, "КВ" №36, 1999).

Я поставил себе куда более скромную задачу: зашифровать 32-битное сообщение. Каково же было мое удивление, когда я обнаружил, что даже зная криптоалгоритм, можно столкнуться с серьезными трудностями при его реализации. Пройдемся по пунктам изложенного выше алгоритма.

Создаем неубывающий массив в 32 элемента. А как подобрать два взаимно простых числа? Число m должно быть больше суммы всех элементов массива. Для моего массива в числе m оказалось 10 значащих цифр. У взаимно простых чисел не должно быть общих делителей, кроме 1. Значит, нужно факторизовать, т.е. разложить на простые множители, оба числа m и w. Время, потраченное на факторизацию 10-значного числа, заставило меня погрустнеть. Пришлось добавить в программу код для сохранения промежуточных результатов и считать в несколько заходов, т.к. оставить считающую программу более чем на четыре часа на рабочем месте так и не удалось. Наконец, два числа m и w факторизованы, и, ура, они взаимно простые. Подобрать число u после "крещения" факторизацией труда не составило. Вооруженный всеми тремя "Мэркли-Хеллмановскими" числами, я тут же мстительно зашифровал тестовое 32-битное сообщение. Расшифровка мне сложной совсем не казалась. Поэтому, расшифровав сообщение и получив (о, ужас!) неправильный результат, мне захотелось выбросить монитор в окно и переквалифицироваться в управдомы. Когда первоначальный шок прошел, удалось выяснить, что "узким местом" было вычисление числа P = S*u mod m. Не помещается его значение в Int64.

Не беда, подумалось мне, объявим его как Extended. Однако это тоже не помогло. Порядок числа с плавающей запятой очень велик, а вот количество значимых цифр в мантиссе ограничено (19-20). Происходит потеря точности, что и приводит к ошибке расшифровки. Вот тут-то и вспомнились предостережения Быченкова А.В. о том, что "практическая реализация алгоритмов (RSA и Эль-Гамаль) требует решения таких проблем, как быстрое выполнение вычислений с числами, состоящими из сотен двоичных разрядов". У меня всего-то 32-разрядные числа, а уже проблема. Так не хотелось использовать встроенный в Delphi аssembler ради перемножения двух больших чисел, что сами собой написались строки на Pascal.

var
 i, j: integer;
 P, Sum: Int64;
 partU, restU: Int64;
 partSum, restSum: Int64;

 partU:= u div 10;
 restU:= u mod 10;
 partSum:= Sum div 10;
 restSum:= Sum mod 10;
 P:= 0;
 for j:= 1 to 10 do begin
 for i:= 1 to 10 do begin
 P:= P + partSum * partU;
 P:= P mod m;
 end;
 P:= P + partSum * restU;
 P:= P mod m;
 end;
 for i:= 1 to 10 do begin
 P:= P + restSum * partU;
 P:= P mod m;
 end;
 P:= P + restSum * restU;
P:= P mod m;

Приведенный выше кусочек кода позволил правильно вычислить число Р и, как следствие, получить верный результат при расшифровке.

Игорь ИВАНОВ-БАККАР