(Окончание. Начало в №1)

Интегралы

Для нахождения определенных интегралов в системе используется функция intg. В самом простом виде функция имеет такой синтаксис:

intg(f, xmin, xmax)

где f - подынтегральное выражение в виде текстовой строки или функция пользователя, xmin и xmax - это соответственно нижний и верхний пределы интегрирования.

Результат работы функции можно записать в переменную.

Напомним, что функция пользователя строится по определенным правилам: начинается с ключевого слова "function", после которого через запятую записывается имя функции, затем сама функция, а заканчивается описание функции пользователя ключевым словом "endfunction".

После этого достаточно вызывать функцию intg, которая возвращает значение определенного интеграла.

Например:

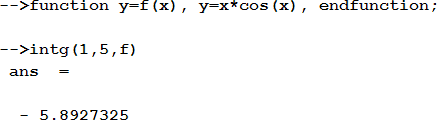
Кроме функции intg система имеет еще несколько функций для нахождения определенных интегралов:

• intsplin - интегрирование при помощи сплайновой интерполяции;
• inttrap - интегрирование при помощи метода трапеций;
• integrate - интегрирование квадратурою.

Решение дифференциальных уравнений

Решение дифференциальных уравнений или систем дифференциальных уравнений в системе может осуществляться только в численном виде.

Для решения применяется функция ode, которая в самом простом виде имеет такой синтаксис:

ode(y₀,x₀,C,f)

где

y₀ - начальное условие: вещественное число для одного дифференциального уравнения или вектор для системы дифференциальных уравнений;

x₀ - начальное значение интервала интегрирования: действительное число для одного дифференциального уравнения или вектор для системы дифференциальных уравнений;

C - координаты оси x в виде: "начальная координата: шаг: конечная координата";

f - функция пользователя - правая часть уравнения или системы уравнений.

Результатом работы функции является множество полученных численных значений решения.

Пример. Найти общее решение обычного дифференциального уравнения первого порядка y' - 10x = 0 на интервале [2,10] с начальным условием y₀ = -1.

Решение состоит в следующей последовательности команд:

В первой строке формируется функция пользователя, на которую в функции ode осуществляется ссылка. Поскольку она должна представлять собой правую часть дифференциального уравнения, то начальное уравнение преобразуется в вид y' = 10x. Во второй строке задаются начальное условие y₀ = -1 и начальное значение интервала интегрирования, а в третьей - интервал изменения независимой переменной [2,10].

Получим графическое решение дифференциального уравнения.

Как нетрудно заметить, координатная сетка для оси x как раз и отображает интервал ее изменения [2,10].

Следует иметь в виду, что начальное значение x₀ должно быть меньше начального значения координаты оси x. В противном случае система генерирует ошибку наподобие приведенной ниже:

Как было отмечено выше, функция ode может быть использована для решения систем дифференциальных уравнений.

Пример. Решить систему дифференциальных уравнений на интервале с начальными условиями y₀ = 0 и z₀ = 0.

Решение будет состоять из такой последовательности команд:

Как видим, во время решения систем дифференциальных уравнений единственным отличием по сравнению с решением отдельных дифференциальных уравнений является создание двух векторов: правых частей уравнений (difur) и начальных условий (y0).

Scilab позволяет настроить "под себя" параметры вычисления для решения дифференциальных уравнений. Для этого он имеет специальное средство, обращение к которому осуществляется командою odeoptions(). Обратите внимание на то, что название команды вводится именно маленькими буквами. После обращения к функции появится диалоговое окно, в котором пользователь и задает соответствующие параметры вычисления для решения дифференциальных уравнений. Верхняя часть окна содержит информацию про назначения и значения по умолчанию, используемые системой для решения дифференциальных уравнений.

Выше было рассмотрено самое простое применение функции ode. Но она имеет достаточно большое количество аргументов, которые заметно увеличивают возможности пользователя для решения дифференциальных уравнений. Например, автоматически в процессе решения Scilab осуществляет выбор между методом прогнозирования и коррекции (nonstiff predictor - corrector) для нежесткой задачи и методом BDF (Backward Differentiation Formula) Адамса-Мултона для жестких задач. Вместе с тем, система позволяет и самостоятельно задать нужный метод. Для этого в функции используется специальный аргумент, записываемый первым в списке аргументов в символьном виде в двойных кавычках, например "adams".

Система предлагает несколько методов, в частности:

• rk4 - адаптивный метод Рунге-угла 4-го порядка;
• rkf - основывается на методе Рунге-Кута-Фельберга (Fehlberg's Runge - Kutta) 4-5-го порядка точности с автоматической оценкой погрешности;
• fix - метод Рунге-угла с фиксированным шагом.

XCOS - моделирование динамических систем

В составе системы имеется модуль Xcos, при помощи которого можно строить динамические модели. Доступ к нему осуществляется командою Инструменты > Визуальное моделирование XCOS, после чего появляется окно нового документа "Untitled" модуля Xcos и окно с палитрой инструментов моделирования.

Построение модели осуществляется в окне "Untitled" с использованием инструментов окна с палитрой инструментов моделирования.

Scilab содержит библиотеку примеров построения моделей в разных отраслях, что дает возможность пользователям уяснить принципы построения моделей. Доступ к примерам осуществляется командою Справка > Примеры XCOS и последующим выбором в окне с примерами группы "XCOS". Примеры моделей сгруппированы по их функциональному назначению, например, "Electrical Systems" (электрические системы), "Control Systems" (системы управления) и т.п. Для выбора конкретной модели следует дважды щелкнуть на ее названии, что приведет к появлению окна с моделью.

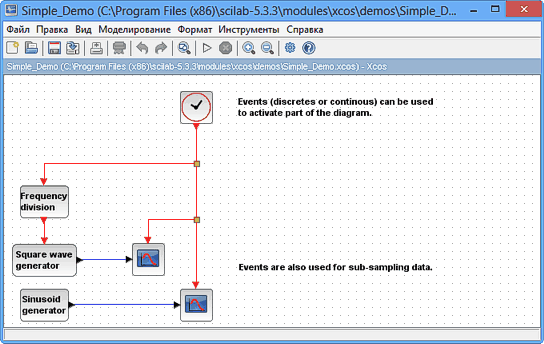
Для запуска модели на выполнение в этом окне следует выполнить команду Моделирование > Выполнить, что приведет к появлению графического окна, в котором и будет отображаться процесс моделирования.

В целом же тема работы с модулем Xcos является сама по себе очень емкой и заслуживает отдельного рассмотрения.

Валерий ФЕТИСОВ