Фрактальная снежинка - один из самых известных и загадочных геометрических объектов - описана Хельгой фон Кох еще в начале нашего века. По традиции ее называют у нас в литературе снежинкой Коха. Это очень "колючая" геометрическая фигура, которую метафорически можно рассматривать как результат многократного "умножения" звезды Давида на саму себя. Шесть ее основных лучей покрыты бесконечным количеством больших и малых вершин-"иголочек". Всякий микроскопический фрагмент контура снежинки как две капли воды похож на весь большой луч, а большой луч в свою очередь содержит в себе бесконечное количество таких же микроскопических фрагментов.
На международном симпозиуме по методологии математического моделирования в Варне еще в 1994 году мне на глаза попалась работа болгарских авторов, которые описывали свой опыт использования снежинки Коха и других подобных объектов на уроках в старших классах для иллюстрации проблемы делимости пространства и философских апорий Зенона. Помимо этого, с образовательной точки зрения весьма интересен, на мой взгляд, сам принцип построения регулярных фрактальных геометрических структур - принцип рекурсивного умножения базового элемента. Природа недаром "любит" фрактальные формы. Это объясняется именно тем, что они получаются путем простого размножения и изменения размеров некого одного элементарного строительного блока. Как известно, природа не излишествует разнообразием причин и, где возможно, обходится наиболее простыми алгоритмическими решениями. Присмотритесь внимательно к контурам листьев, и во многих случаях вы обнаружите явное их родство с формой контура снежинки Коха.
Визуализация фрактальных геометрических структур возможна лишь при помощи компьютера. Построить снежинку Коха выше третьего порядка вручную уже очень сложно, а заглянуть в бесконечность так хочется! Поэтому, почему бы ни попытаться разработать соответствующую компьютерную программу. В РуНете можно отыскать рекомендации строить снежинку Коха из треугольников. Результат работы этого алгоритма выглядит как нагромождение пересекающихся линий. Интереснее скомбинировать эту фигуру из "кусочков". Контур снежинки Коха состоит из отрезков одинаковой длины, наклоненных под углом 0°, 60° и 120° по отношению к горизонтальной оси x. Если обозначить их соответственно 1, 2 и 3, то снежинка любого порядка будет состоять из следующих друг за другом троек - 1, 2, 3, 1, 2, 3, 1, 2, 3… и т. д. Каждый из этих трех типов отрезков может прикрепляться к предыдущему одним либо другим концом. С учетом этого обстоятельства можно считать, что контур снежинки состоит из отрезков шести типов. Обозначим их 0, 1, 2, 3, 4, 5. Таким образом, мы получаем возможность кодировать контур любого порядка при помощи 6 цифр (см. рисунок).
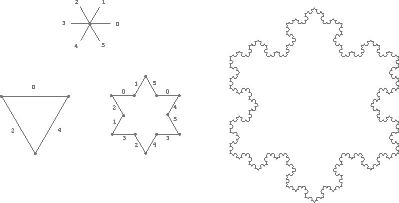
Снежинка более высокого порядка получается из предшественницы более низкого порядка путем замены каждого ребра на четыре, соединенных подобно сложенным ладошкам (_/\_). Ребро типа 0 заменяется на четыре ребра 0, 5, 1, 0 и так далее в соответствии с таблицей:
| 0 | 0 1 5 0 |
| 1 | 1 2 0 1 |
| 2 | 2 3 1 2 |
| 3 | 3 4 2 3 |
| 4 | 4 5 3 4 |
| 5 | 5 0 4 5 |
Простой равносторонний треугольник можно рассматривать как снежинку Коха нулевого порядка. В описанной системе кодировки ему соответствует запись 0, 4, 2. Все остальное можно получить путем описанных замен. Я не буду приводить здесь код процедуры и тем самым лишать вас удовольствия разработать свою программу самостоятельно. При ее написании вовсе необязательно использовать явный рекурсивный вызов. Его можно заменить обычным циклом. В процессе работы у вас будет лишний повод поразмыслить о рекурсии и ее роли в образовании квазифрактальных форм окружающего нас мира, а в конце пути (если, конечно, не поленитесь пройти его до конца) вы сможете полюбоваться сложным узором контуров фрактальной снежинки, а также заглянуть, наконец, в лицо бесконечности.
А. КОЛЕСНИКОВ,
[email protected]










